In my article where I introduced the Range library that came with the C++20 standard, I discussed the library’s lazy evaluation approach and the benefits it brings to the language. While introducing the Range library, I attempted to convey its adapters and generators through practical examples without diving into technical details. However, understanding the Range library without understanding the concept of lazy evaluation can be challenging. Therefore, I’d like to talk to you about lazy evaluation and how the Range library enables it.
TL;DR
Lazy evaluation is a crucial concept in C++ that allows us to delay computations until they are genuinely needed, potentially improving code performance. This article introduces lazy evaluation, explains its benefits, and shows how C++11 and later versions have made it more accessible. By using a simple multiply function example, we illustrate the power of lazy evaluation in minimizing unnecessary calculations. Lazy evaluation is not just for numerical computations; it also plays a role in C++20’s std::ranges library, offering deferred algorithm execution. Understanding lazy evaluation can help you write more efficient, resource-friendly code in C++
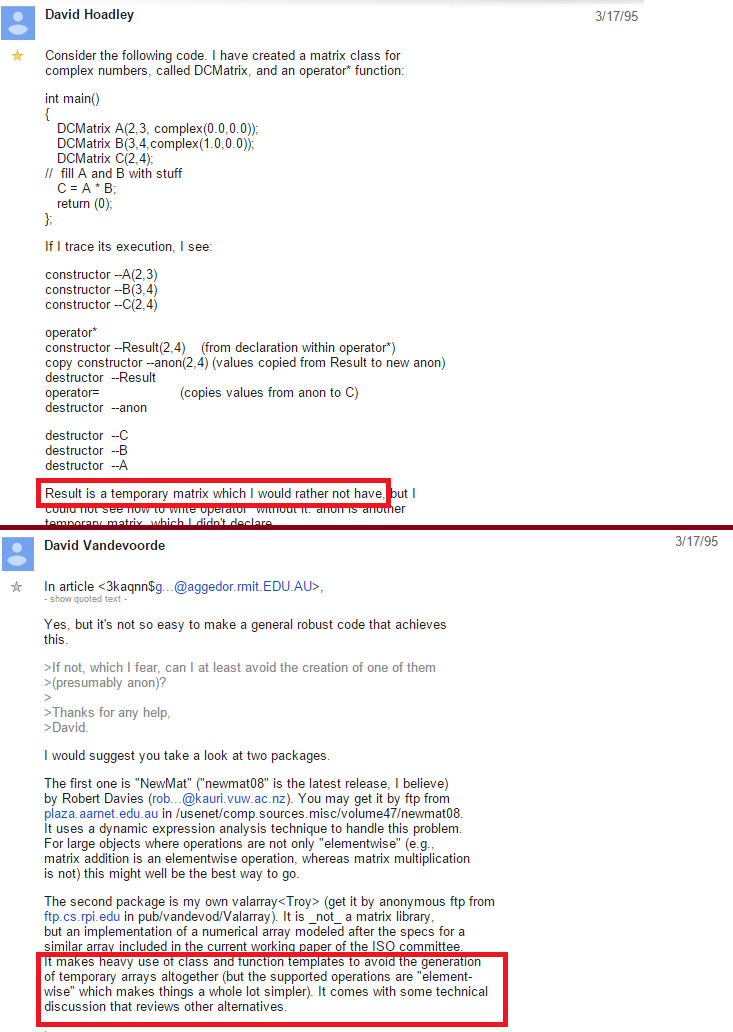
Lazy evaluation, which was first introduced in 1995 with the Expression Templates technique, is a core architectural concept in numerical computation libraries like Blaze, Boost.UBlas, and Blitz. Despite its simple underlying structure, lazy evaluation can have a significant impact on performance.
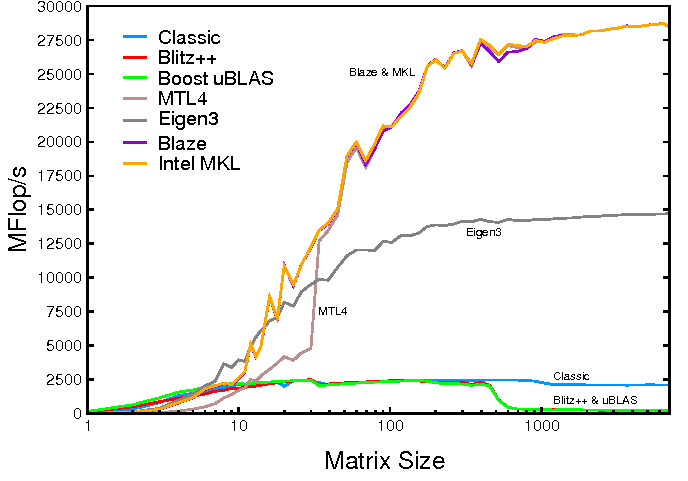
Although lazy evaluation has been known for a long time, it was not widely adopted by developers until the introduction of C++11 and later versions. This is because C++11 introduced a number of features that simplified the syntax of lazy evaluation, such as the auto type deducer, variadic templates, and lambda expressions. These features made it easier for developers to write and understand code that uses lazy evaluation, making it a more accessible option for a wider range of projects
Eager Evaluation - Immediate Computation
When we design our code, we typically assume that the code will be executed immediately when it is written. This is because it makes our code easier to read and debug. The immediate computation method is a programming technique that enforces this assumption. It ensures that the code is executed at the point of invocation, which can lead to more deterministic and controlled behavior.
When we write a function int multiply(int x, int y) that performs a multiplication operation, the structure of the function which uses immediate computation will be as follows:
1. int multiply(int x, int y) { return x * y; }
2.
3. int main() {
4. int x = 2, y = 3;
5. int tmp = multiply(x, y);
6. int result = multiply(4, tmp);
7. // ... and many other calculations ...
8. cout << "result: " << result << "\n";
9. }
In immediate computation, the multiply function will instantly calculate the product of the given values and assign the result to the tmp variable at line 5.. Then, it will use the calculated temporary variable to perform the remaining multiplication operation and assign the result to the result variable. Although the calculated result value may not be used until it is printed to the console, it is holds within the application until line 8..
Lazy Evaluation - Lazy Computation Architecture
If the multiply function were written with lazy evaluation, the multiplications would be deferred until they were needed. This means that the code would not actually multiply the numbers until the value was needed on line 8.. In the new approach, the result variable would not actually hold the final value of the operations. Instead, it would be a function that would combine all the computations and calculate them one at a time when needed. This could improve performance by avoiding unnecessary calculations.
To achieve lazy evaluation, let’s rewrite our multiply function to return an intermediate object lazy_t<T1, T2> that holds data type and can store the multiplication operations:
template <typename T1, typename T2>
struct lazy_t; // (1)
template <typename T1, typename T2> // (2)
lazy_t<T1, T2> multiply(T1 x, T2 y)
{
return lazy_t<T1, T2>(x , y); // (3)
}
-
We define the intermediate class, named
lazy_t, which will hold the multiplication operations and delay them until the final result is needed. This class will be the main structure used for lazy evaluation, and it will handle all the operations through this class. -
Because we want to combine the multiplication operations, the arguments to the
multiplyfunction can be either integral type or instances of thelazy_tclass from a previous multiplication operation which hold the other multiplication. Therefore, the multiply function must accept different types. As a result, we implement our multiply function within a structure that accepts two different template types -
The
multiplyfunction can simply return thelazy_t<T1, T2>class, which stores the type information of the two arguments. The type information and values held by the resulting class will be used to calculate the final result by combining all the given operations.Note that before the introduction of the
autotype deducer with Modern C++, it was necessary to explicitly define the types of intermediate classes created using the lazy approach.
Writing or defining the types of intermediate classes, even for combinations of two or three operations, was challenging and uninteresting in C++ due to the absence of features that simplify syntax.
Let’s start to implement the lazy_t class, which is returned by the multiply function.
The implementation of the class will be as follows:
template <typename T1, typename T2>
struct lazy_t
{
lazy_t(const T1& first_,
const T2& second_)
: first(first_)
, second(second_) { }
template <typename result_t>
operator result_t() const {
return first * second; // (2)
}
private:
T1 first; // (1)
T2 second; // (1)
};
-
We need to store the received variables in our lazy class; we will use these variables to calculate the result.
-
To have the actual result, the
lazy_tclass provides a cast operator to the integral type using for the calculation. Whenint result = lazy_t<...>;is called, this operator will be called and make the calculations happen.
Let’s put our code together and perform a multiplication operation using the lazy evaluation technique:
1. int main()
2. {
3. int x{ 1 }, y{ 2 }, z{ 3 };
4. auto lazy_y_z = multiply(y, z);
5. auto lazy_x_y_z = multiply(x, lazy_y_z);
6.
7. std::cout << "type of lazy_x_y : "
8. << typeid(lazy_y_z).name() << "\n";
9.
10. std::cout << "type of lazy_x_y_z: "
11. << typeid(lazy_x_y_z).name() << "\n";
12.
13. int result = lazy_x_y_z;
14. std::cout << "result of lazy operations: "
15. << result << "\n";
16. }
8. type of lazy_x_y : struct lazy::lazy_t<int, int>
11. type of lazy_x_y_z: struct lazy::lazy_t<int, struct lazy::lazy_t<int, int> >
14. result of lazy operation: 6
The code we wrote will run successfully, and at the line 13 where we run int result = lazy_x_y_z;, the multiplication operation will take place, assigning the result to the result variable.
However, there is one more step needed to achieve the desired result. When we combine the multiplication operations, the final lazy object will have the type information of the previous lazy object created for the multiplication, instead of an integer.
Therefore, we need to provide the ‘*’ multiplication operator for the lazy<X, Y> class, which is created with an integer type and types X and Y.
template <typename result_t, typename U1, typename U2>
result_t operator*(const result_t& left, const lazy_t<U1, U2>& oth)
{
return left * oth.first * oth.second;
}
Note that the types of
oth.firstoroth.secondvariables can be instances of differentlazy<T1, T2>classes created for previous operations!
In such a case, theoperator*(...)multiplication operator will be recursively called for the relevant multiplication operation, allowing multiplication operations to be completed in a connected manner.
Thanks to the lazy evaluation technique, our multiply function can combine any number of multiplication operations into a single multiplication operation. Although this technique is using mainly in complex calculations for performance improvement, it is also enabling to make std::range library for deferring the computation of the result of an algorithm or view until it is actually needed. This can be beneficial for performance, as it can avoid unnecessary computations.
Using lazy evaluation, our multiply function can combine any number of multiplication operations into a single operation. This technique is commonly used to improve performance in complex calculations, and it is also used in the std::ranges library to defer the computation of the result of an algorithm or view until it is actually needed. This can be beneficial, as it can avoid unnecessary computations.
Lastly, If we combine the code we’ve written, our final code will look like this:
#include <iostream>
template <typename T1, typename T2>
struct lazy_t
{
lazy_t(const T1& first_, const T2& second_)
: first(first_)
, second(second_) { }
template <typename result_t>
operator result_t() const {
return first * second;
}
private:
template <typename result_t, typename U1, typename U2>
friend result_t operator*(const result_t& left,
const lazy_t<U1, U2>& oth);
T1 first;
T2 second;
};
template <typename result_t, typename U1, typename U2>
result_t operator*(const result_t& left,
const lazy_t<U1, U2>& oth)
{
return left * oth.first * oth.second;
}
template <typename T1, typename T2>
lazy_t<T1, T2> multiply(T1 x, T2 y)
{
return lazy_t<T1, T2>(x, y);
}
int main()
{
int x{ 2 }, y{ 2 }, z{ 2 };
auto lazy_result = multiply(x, multiply(y, z));
std::cout << "result of lazy operations: " << int(lazy_result) << "\n";
}